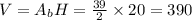Answer:
Depends. See text.
Explanation:
Surface area or volume?
Ther are two options.
Case 1: we know nothing about the green angles I've marked in green. Data is insufficient to determine the perimeter of the trapezoid base, and then to calculate the surface area.
Case 2:Unlikely, since the right angles are marked everywhere else when not obvious: the base of the prism is a right trapezoid, ie two of the angles measures 90°. In that case we can easily find the length of the missing side with pythagorean theorem:
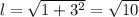 . Perimeter becomes
. Perimeter becomes
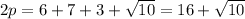 . Base area is
. Base area is
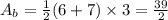 And the total surface becomes
And the total surface becomes

Or is it the volume you want? Way simpler, we calculate the area of the prism (see above) and multiply it by the height of the solid: