Question

Find the area of circle o if DCBO is a rectangle and DB measure 10 units

Answer 1

`100\pi`

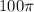
Explanation:

Step 1: Identity the radius.

Since O is the center of the circle, and C and E lie on the circumference, OC and OE are the radii of the circle and thus,

OC=OE.

Step 2: Consider the rectangle.

All diagonals in a rectangle are congruent so this means

DB= OC ( OC is also a diagonal).

Thus, OC= 10 units.

Step 3: Analyze

So this means OE is also 10 units as well.

Since we know the length of the radius, Use the area of circle,

`\pi {r}^(2)`

`\pi( {10}^(2) ) = 100\pi`

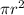
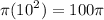
So the area of a circle is 100 pi.

Answer 2

314.2 square units

Explanation:

The diagonals of a rectangle are the same length, so segment OC is the same length as segment DB: 10 units. OC is a radius of the circle, which means the circle's radius is 10 units.

The area of a circle is given by ...

A = πr²

A = π(10 units)² = 100π units²

A ≈ 314.2 units²

The area of circle O is about 314.2 square units.