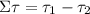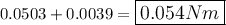Question

A grinding wheel is a uniform cylinder with a radius of 8.50 cm and a mass of 0.380 kg. Calculate (a) its moment of inertia about its center, and (b) the applied torque needed to accelerate it from rest to 1750 rpm in 5.00 s. Take into account a frictional torque that has been measured to slow down the wheel from 1500 rpm to rest in 55.0 s.

Answer 1

Hi there!

(A)

A grinding wheel is the same as a disk, having moment of inertia of:

`I = (1)/(2)MR^2`

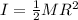
Plug in the given mass and radius (REMEMBER TO CONVERT) to find the moment of inertia:

`I = (1)/(2)(0.380)(0.085)^2 = 0.00137 kgm^2`

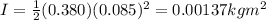
(B)

We can use the rotational equivalent of Newton's Second Law to calculate the needed torque:

Στ = Iα = τ₁ - τ₂

Begin by solving for the angular acceleration. Convert rpm to rad/sec:

`(1750r)/(min) * (1 min)/(60 s) * (2\pi rad)/(1 r) = 183.26 rad/sec`

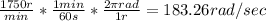
Now, we can use the following equation:

ωf = wi + αt (wi = 0 rad/sec, from rest)

183.26/5 = α = 36.65 rad/sec²

τ = Iα = 0.0503 Nm

Since there is a counter-acting torque on the system, we must begin by finding that acceleration:

`(1500r)/(min) * (1 min)/(60 s) * (2\pi rad)/(1 r) = 157.08 rad/sec`

ωf = wi + αt

-157.08/55 = α = -2.856 rad/sec²

τ₂ = Iα = 0.0039 Nm

Now, calculate the appropriate torque using the above equation:

`\Sigma\tau = \tau_1 - \tau_2`

`\Sigma\tau + \tau_2 = \tau_1`

`0.0503 + 0.0039 = \large\boxed{0.054 Nm}`