Answer:
![\left[A]](https://img.qammunity.org/2022/formulas/mathematics/high-school/4a3xinim4uc2ecfalonjcs2qrh0o45to9u.png) The ratios
The ratios
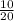 form a proportion by common multiplier 3 to get
form a proportion by common multiplier 3 to get
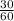
![\left[B]](https://img.qammunity.org/2022/formulas/mathematics/high-school/zvoilzxf0vw0pxq4r1ta30se8vrzp5ho11.png) Both ratio are equal to
Both ratio are equal to
 in simplest form
in simplest form
Explanation:
![\left[A]](https://img.qammunity.org/2022/formulas/mathematics/high-school/4a3xinim4uc2ecfalonjcs2qrh0o45to9u.png) We need to show both fraction of same proportion.
We need to show both fraction of same proportion.
Ratio 1:
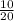
If we multiply by 3 at numerator and denominator
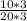
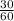
Therefore
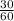 is equivalent ratio to second one 30/60
is equivalent ratio to second one 30/60
Hence, The ratio 10/20 form a proportion by common multiplier 3 to get 30/60
∴-----------------------------------------------------------------------------------------------------∴
![\left[B]](https://img.qammunity.org/2022/formulas/mathematics/high-school/zvoilzxf0vw0pxq4r1ta30se8vrzp5ho11.png) Now we simplify both ration into simplest form
Now we simplify both ration into simplest form
→
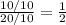
→
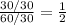
→
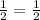
Hence, Both ratio are equal to
 in simplest form.
in simplest form.