There are 100 numbers in the range 100-199. Find the smallest and largest multiple of 13 in this range. We have
104 = 8•13
195 = 15•13
so there are 15 - 8 + 1 = 8 multiples of 13 between 100 and 199.
Then the sum we want is
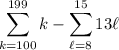
or equivalently,
(100 + 101 + 102 + … + 199) - 13 (8 + 9 + … + 15)
To compute these sums, recall the following formula:
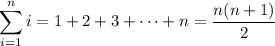
Then
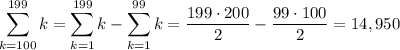
and
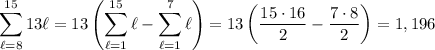
which means the sum we want is 14,950 - 1,196 = 13,754.