Question

Complete the statements about the linear equation 10x + 4y =

-20. Enter the intercepts as Coordinate points.
The x-intercept is
choose your answer...
and the y-intercept is
choose your answer.…

Answer 1

x-intercept: (-2, 0)

y-intercept: (0, -5)

Explanation:

Note:

Since the options were not included in the original post, I will be providing the solutions (coordinates of the intercepts).

Given the linear equation in standard form, 10x + 4y = -20, where we must determine the x- and y-intercepts of the graph:

X-intercept:

The x-intercept, in the form (a, 0), is the point on the graph where it crosses the x-axis. Thus, it is the value of x when its corresponding y-coordinate is: y = 0.

In order to find the x-intercept, set y = 0 and solve for the value of x:

10x + 4y = -20

10x + 4(0) = -20

10x + 0 = -20

10x = -20

Divide both sides by 10 to solve for x:

`\displaytext\mathsf{(10x)/(10)\:=\:(-20)/(\:10)}`

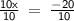
x = -2

Hence, the x-intercept is (-2, 0).

Y-intercept:

The y-intercept, in the form (0, b ), is the point on the graph where it crosses the y-axis. Thus, it is the value of y when its corresponding x-coordinate is: x = 0.

In order to find the y-intercept, set x = 0 and solve for the value of y:

10x + 4y = -20

10(0) + 4y = -20

0 + 4y = -20

Divide both sides by 4 to solve for y:

`\displaytext\mathsf{(4y)/(4)\:=\:(-20)/(\:4)}`

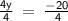
y = -5

Hence, the y-intercept is (0, -5).