Question

Help me please!! This is timed and I’m stuck

Answer 1

B 13/2

Explanation:

2x² + 7x - 15 = 0

First we want to find the two solutions

We can do this by using the quadratic formula

Quadratic formula:

`\frac{- b + or - \sqrt{b {}^(2) - 4(a)(c)} }{2(a)}`

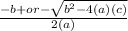
Where the values of a,b and c are derived from the equation.

The equation is put in ax² + bx + c = 0 form

2x² + 7x - 15 = 0

so a = 2, b = 7 and c = - 15

We now plug these values into the quadratic formula

(-(7) + or - √7² - 4(2)(-15) ) / 2(2)

first solution: -(7) + √7² - 4(2)(-15) ) / 2(2)

remove parenthesis on 7

(-7 + √7² - 4(2)(-15) ) /2(2)

Apply exponents 7²

(-7 + √49 - 4(2)(-15) ) /2(2)

Multiply -4,2 and -15

(-7 + √49 + 120 ) / 2(2)

add 49 and 120

(-7 + √ 169 ) / 2(2)

Take square root of 169

(-7 + 13 ) / 2(2)

add 13 and -7

6/2(2)

multiply 2 and 2

= 6/4

The first solution is 6/4 or 1.5

Now the second solution: -(7) - √7² - 4(2)(-15) ) / 2(2)

For the second solution we basically go through the same steps as for finding the first solution, the only difference is instead of adding -b and √b² - 4(a)(c) we are subtracting.

So we would have ( -7 - 13 ) / 2(2) instead of (-7+13)/2(2)

So second solution: ( -7 - 13 ) / 2(2)

subtract 13 from -7

-20/2(2)

multiply 2 and 2

-20/4

divide

The second solution is -5

Now that we have found the solutions we want to find r - s if r and s are the solutions to the equation and that r > s

The two solutions are 6/4 and -5.

6/4 > -5 so we know that r must equal 6/4 and s must equal -5 because r has to be greater than s

So if r = 6/4 and s = -5

Then r - s = 6/4 - (-5) = 6/4 + 5 = 13/2

So the answer is B. 13/2