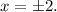Question

Find the maximum and minimum of g(x)= x^2-3x+4/x^2+3x+4

Answer 1

Explanation:

To find the maxima/minima of a function, we solve for the derivative of the given function

`g(x) = (x^2 - 3x + 4)/(x^2 + 3x + 4)`

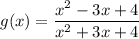
Recall that according to the quotient rule of differentiation, if a function g(x) is defined as a ratio of two functions f(x) and h(x), then the derivative of g(x) is

`g'(x) = (f'(x)h(x) - f(x)h'(x))/([g(x)]^2)`

Let

`f(x) = x^2 - 3x + 4 \Rightarrow f'(x) = 2x - 3`

`h(x) = x^2 + 3x + 4 \Rightarrow g'(x) = 2x + 3`

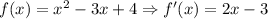
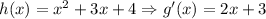
The derivative g')x) is then

`g'(x) = ((2x - 3)(x^2 + 3x + 4) - (2x + 3)(x^2 - 3x + 4))/((x^2 + 3x + 4)^2)`

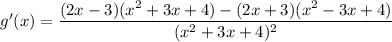
Carrying out the multiplication and collecting all similar terms, we arrive at

`g'(x) = (6(x^2 - 4))/((x^2 + 3x + 4)^2)`

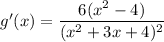
The maxima/minima of the function g(x) occurs where g'(x) = 0 and this happens when the numerator of g'(x) is

`x^2 - 4 = 0 \Rightarrow x = \pm2`

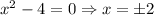
Look at the graph above. The blue line represents the function g(x) and the red line is for the derivative of g(x) and you can clearly see that maxima/minima occurs when the red line intersects the horizontal axis, i.e., becomes zero at
`x = \pm2.`