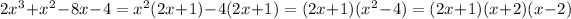Answer:
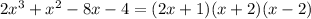
Explanation:
Let's collect
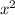 between the first two terms, and -4 between the last two:
between the first two terms, and -4 between the last two:
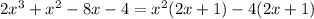
At this point you should see there is a common factor
 between both terms, then let's collect that:
between both terms, then let's collect that:
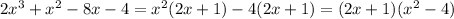
Final step is recognizing a difference of squares (x and 2) in the second bracket, to end up our work!