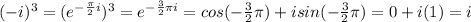Answer:
B: i
Explanation:
Algebric explanation: as long as you remember power rules you should be good:
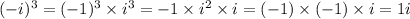
Geometric explanation: In the complex plane you can think "multiplying by i" as "rotate 1/4 counterclockwise".
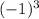 is a real number, and it's simply
is a real number, and it's simply
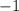 . Rotate that ccw once, you're at
. Rotate that ccw once, you're at
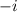 . Again, and you're at 1. third time (is really the charm!) you end up at
. Again, and you're at 1. third time (is really the charm!) you end up at
 .
.
Polar explanation Courtesy of euler's identity.