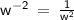Answer:
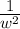
Explanation:
Given the exponential expression,
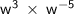 , where it involves the multiplication of the same base, w, with varying powers.
, where it involves the multiplication of the same base, w, with varying powers.
Using the Product Rule of Exponents, where it states that,
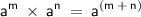 .
.
Hence, we simply need to add the exponents:
![\displaytext\mathsf{w^3\:*\:w^(-5)\:=\:w\:^([3\:+\:(-5)])\:=\:w^(-2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/h6b3ak5u7elsj388egoin11ccclghmkc0k.png)
Next, apply the Negative Exponent Rule, where it states that:
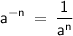 .
.
Transforming the negative exponent of
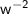 becomes a positive exponent by using the Negative Exponent Rule.
becomes a positive exponent by using the Negative Exponent Rule.