Question

I need help because all the answer choices my teacher put were wrong so I dont know what to do ​

Answer 1

Equivalent Expression:
`\displaytext\mathsf{(a^7)/(b^8)}`

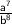
Explanation:

Given the exponential expression,
`\displaystyle\mathsf{(a^(12)\:b^(-3))/(a^(5)\:b^(5))}`:

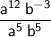We could use the Quotient Rule of Exponents where it states that:

`\displaystyle\mathsf{(a^m)/(a^n)\:=\:a^((m\:-\:n))}`

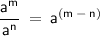
Since we have the variables, a and b as the base, we could simply apply the Quotient Rule and subtract their exponents.

`\displaystyle\mathsf{(a^(12)\:b^(-3))/(a^(5)\:b^(5))\:=\:a^((12\:-\:5))\:b^((-3\:-\:5))}`

`\displaytext\mathsf{=\:a^(7)\:b^(-8)}`

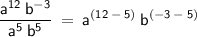
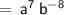
Next, we must transform the negative exponent of base, b, into positive by applying the Negative Exponent Rule, where it states that:

`\large\text{$ a^(-n)\:=\:(1)/(a^(n)) $}`

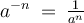
Applying the Negative Exponent Rule will result in the following exponential expression:

`\LARGE\text{$ a^(7)\:b^(-8)\:=\:[a^(7)\:*\:(1)/(b^8)]\:=\:(a^7)/(b^8) $}`

Therefore, the equivalent expression is:
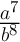`\LARGE\text{$ (a^7)/(b^8) $}`.