Sketch the graph of y=x^2-4x+3

Question

asked Dec 12, 2023 29.1k views

1 Answer

Chitresh · Answer 1 · 2023-12-18T00:33:02+0000

Answer:

see attached graph

Explanation:

Given equation:
y=x^2-4x+3

Standard form of a quadratic equation:
y=ax^2+bx+c

where
is the y-intercept

If
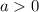a > 0 then the parabola opens upwards.

If
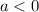a < 0 then the parabola opens downwards.

Therefore, the y-intercept of the graph is (0, 3)

To find the x-intercepts, factor the equation:

y=x^2-4x+3

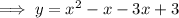
$\implies y=x^2-x-3x+3$

$\implies y=x(x-1)-3(x-1)$

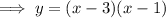
$\implies y=(x-3)(x-1)$

Therefore, the x-intercepts of the graph are (3, 0) and (1, 0)

To determine the vertex, differentiate the equation:

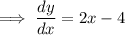
$\implies (dy)/(dx)=2x-4$

Set to zero and solve for x:

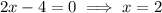
$2x-4=0 \implies x=2$

Substitute
x=2 into the original equation and solve for y:

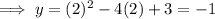
$\implies y=(2)^2-4(2)+3=-1$

Therefore, the vertex (or turning point) is at (2, -1)