Answer:
Width = 43 feet
Explanation:
Given the 188-feet perimeter of a rectangular garden, for which its length is 8 feet longer than its width:
We can express the length of the rectangular garden as: 8 + W.
Hence, in order to solve for the length and the width of the rectangular garden, use the following formula for the perimeter of a rectangle:
Perimeter (P) = 2(L + W) or 2L + 2W = 188 feet
Length (L) = 8 + W
Width (W) = W
Substitute these values into the perimeter formula to solve for the value of the rectangular garden's dimensions:
P = 2L + 2W
188 feet = 2(8 + W) + 2W
Distribute 2 into the parenthesis, (8 + W):
188 = 16 + 2W + 2W
Combine like terms:
188 = 16 + 4W
Subtract 16 from both sides:
188 - 16 = 16 - 16 + 4W
172 = 4W
Divide both sides by 4 to solve for W:
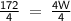
W = 43
Therefore, the width of a rectangular garden is 43 feet.
Since we determined that the length is 8 + W, then it means that the length of the rectangular garden is 51 feet.
Verify the dimensions:
Double-check whether we have the correct dimensions for the rectangular garden by substituting the length (L) = 51 feet, and the width (W) = 43 feet, into the perimeter formula:
P = 2L + 2W
188 feet = 2(51) + 2(43)
188 feet = 102 + 86
188 feet = 188 feet (True statement). This means that we have the correct dimensions for the rectangular garden.
Answers:
Therefore, the width of a rectangular garden is 43 feet.