Given -
➙ a quadratic equation in which Harry lagged due to an error made by him, 2x² - x - 6= 0
To solve -
➙ the given quadratic equation.
Concept applied -
➙ We will apply the quadratic formula as given in the question. So, let's study about quadratic equation first because we are supposed to apply the formula in equation.
What is quadratic equation?
➙ A quadratic equation in the variable x is an equation of the form ax² + bx + c = 0, where a, b, c are real numbers, a ≠ 0.
Now, what is quadratic formula?
➙The roots of a quadratic equation ax + bx + c = 0 are given by
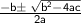 provided b - 4ac ≥ 0.
provided b - 4ac ≥ 0.
Solution -
here as per the given quadratic equation,
a = 2, b = -1 and c = -6
putting in the formula,
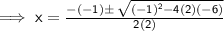
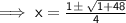
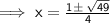
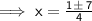
Solving one by one,
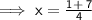
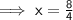
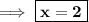
________________
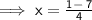
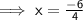
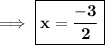
________________________________
Note - Hey dear user!! You haven't provided the solution which was solved by Harry (A.T.Q). Please go through the solution as it will help you to find the error done by Harry.
________________________________
Hope it helps!! (: