To solve
 , isolate the absolute value, create two cases, and combine solutions. The correct answer is
, isolate the absolute value, create two cases, and combine solutions. The correct answer is
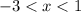 , and the appropriate choice is D.
, and the appropriate choice is D.
Let's solve the inequality step by step:
![\[3|x + 1| < 6\]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/hir97n7ttovj7fp0f6k6.png)
1. Isolate the Absolute Value:
![\[ |x + 1| < 2 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/7lzxr0527uuugn8ll77s.png)
2. Create Two Cases:
- Case one:
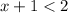
![\[ x < 1 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/dwnalpb08808ez47xiao.png)
- Case two:

![\[ x > -3 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/weuznb307g4no8qaokp2.png)
3. Combine the Solutions:
- Combine the solutions from both cases:
![\[ -3 < x < 1 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ynze2ni7xi0i3a3u5zma.png)
Now, let's look at the choices:
A.
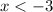 or
or
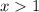 - Incorrect
- Incorrect
B.
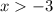 and
and
 - Incorrect
- Incorrect
C.
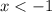 or
or
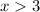 - Incorrect
- Incorrect
D.
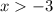 and
and
 - Correct (it marks the interval from -
- Correct (it marks the interval from -
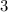 to
to
 )
)
So, the correct solution is
 , and D marks the interval from -
, and D marks the interval from -
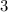 to
to
 , so D is the correct choice.
, so D is the correct choice.