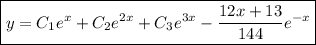Question

Differential Equation

Answer 1

1. The given equation is probably supposed to read

y'' - 2y' - 3y = 64x exp(-x)

First consider the homogeneous equation,

y'' - 2y' - 3y = 0

which has characteristic equation

r² - 2r - 3 = (r - 3) (r + 1) = 0

with roots r = 3 and r = -1. Then the characteristic solution is

`y = C_1 e^(3x) + C_2 e^(-x)`

and we let y₁ = exp(3x) and y₂ = exp(-x), our fundamental solutions.

Now we use variation of parameters, which gives a particular solution of the form

`y_p = u_1y_1 + u_2y_2`

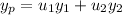
where

`\displaystyle u_1 = -\int (64xe^(-x)y_2)/(W(y_1,y_2)) \, dx`

`\displaystyle u_2 = \int (64xe^(-x)y_1)/(W(y_1,y_2)) \, dx`

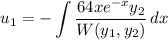
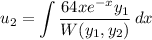
and W(y₁, y₂) is the Wronskian determinant of the two fundamental solutions. This is

`W(y_1,y_2) = \begin{vmatrix}e^(3x) & e^(-x) \\ (e^(3x))' & (e^(-x))'\end{vmatrix} = \begin{vmatrix}e^(3x) & e^(-x) \\ 3e^(3x) & -e^(-x)\end{vmatrix} = -e^(2x) - 3e^(2x) = -4e^(2x)`

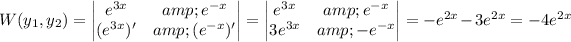
Then we find

`\displaystyle u_1 = -\int (64xe^(-x) \cdot e^(-x))/(-4e^(2x)) \, dx = 16 \int xe^(-4x) \, dx = -(4x + 1) e^(-4x)`

`\displaystyle u_2 = \int (64xe^(-x) \cdot e^(3x))/(-4e^(2x)) \, dx = -16 \int x \, dx = -8x^2`

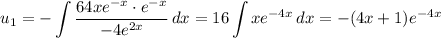
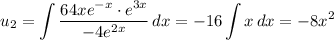
so it follows that the particular solution is

`y_p = -(4x+1)e^(-4x) \cdot e^(3x) - 8x^2\cdot e^(-x) = -(8x^2+4x+1)e^(-x)`

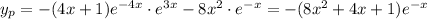
and so the general solution is

`\boxed{y(x) = C_1 e^(3x) + C_2e^(-x) - (8x^2+4x+1) e^(-x)}`

2. I'll again assume there's typo in the equation, and that it should read

y''' - 6y'' + 11y' - 6y = 2x exp(-x)

Again, we consider the homogeneous equation,

y''' - 6y'' + 11y' - 6y = 0

and observe that the characteristic polynomial,

r³ - 6r² + 11r - 6

has coefficients that sum to 1 - 6 + 11 - 6 = 0, which immediately tells us that r = 1 is a root. Polynomial division and subsequent factoring yields

r³ - 6r² + 11r - 6 = (r - 1) (r² - 5r + 6) = (r - 1) (r - 2) (r - 3)

and from this we see the characteristic solution is

`y_c = C_1 e^x + C_2 e^(2x) + C_3 e^(3x)`

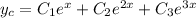
For the particular solution, I'll use undetermined coefficients. We look for a solution of the form

`y_p = (ax+b)e^(-x)`

whose first three derivatives are

`{y_p}' = ae^(-x) - (ax+b)e^(-x) = (-ax+a-b)e^(-x)`

`{y_p}'' = -ae^(-x) - (-ax+a-b)e^(-x) = (ax-2a+b)e^(-x)`

`{y_p}''' = ae^(-x) - (ax-2a+b)e^(-x) = (-ax+3a-b)e^(-x)`

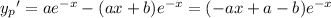
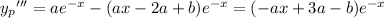
Substituting these into the equation gives

`(-ax+3a-b)e^(-x) - 6(ax-2a+b)e^(-x) + 11(-ax+a-b)e^(-x) - 6(ax+b)e^(-x) = 2xe^(-x)`

`(-ax+3a-b) - 6(ax-2a+b) + 11(-ax+a-b) - 6(ax+b) = 2x`

`-24ax+26a-24b = 2x`

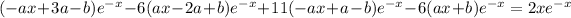
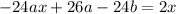
It follows that -24a = 2 and 26a - 24b = 0, so that a = -1/12 = -12/144 and b = -13/144, so the particular solution is

`y_p = -(12x+13)/(144)e^(-x)`

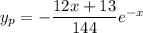
and the general solution is

`\boxed{y = C_1 e^x + C_2 e^(2x) + C_3 e^(3x) - (12x+13)/(144) e^(-x)}`