Question

Please can you help me x

Answer 1

PX : XQ = 2 : 5

Explanation:

Since RX is perpendicular to PQ , then

Δ RPX and Δ RQX are right triangle

Calculate PX and XQ using Pythagoras' identity in the right triangles

PX² = 20² - 16² = 400 - 256 = 144 ( take square root of both sides )

PX =
`√(144)` = 12

Similarly

XQ² = 34² - 16² = 1156 - 256 = 900 ( take square root of both sides )

XQ =
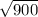`√(900)` = 30

Then

PX : XQ = 12 : 30 = 2 : 5 ( in simplest form )