Question

Silver can be plated out of a solution containing Ag+ according to the half-reaction

Ag+(aq)+e−→Ag(s)


How much time (in minutes) does it take to plate 19 g of silver using a current of 3.4 A ?

Answer 1

Approximately
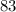`83` minutes.

Step-by-step explanation:

Look up the relative atomic mass of
`\rm Ag`:
`M({\rm Ag}) = 107.868\; \rm g \cdot mol^(-1)`.
`\begin{aligned}Q &= e\, (n(e)) \\ &\approx 1.602 * 10^(-19)\; \rm C * 1.06 * 10^(23) \\ &\approx 1.6987 * 10^(4)\; \rm C \end{aligned}`/.

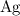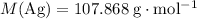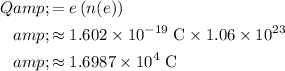Avogadro's number:
`N_A \approx 6.02 * 10^(23)\; \rm mol^(-1)`.

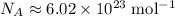Elementary charge:
`e \approx 1.602 * 10^(-19)\; \rm C`.

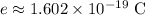Calculate the quantity of
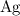`\rm Ag` atoms to reduce:

`\begin{aligned}& n({\rm Ag}) \\ &= \frac{m({\rm Ag})}{M({\rm Ag})} \\ &= (19\; \rm g)/(107.868\; \rm g \cdot mol^(-1)) \\ & \approx 0.176\; \rm mol\end{aligned}`.

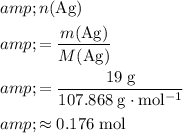By the equation, it takes one electron to reduce every
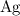`\rm Ag` atom. Thus, the number of electrons required to reduce
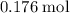`0.176\; \rm mol` of
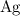`\rm Ag\!` atoms would be:

`n(e) = n({\rm Ag}) \approx 0.176\; \rm mol`.

`\begin{aligned}N(e) &= n(e) \cdot N_(A). \\ &\approx 0.176\; \rm mol * 6.02 * 10^(23)\; \rm mol^(-1) \\ & \approx 1.06 * 10^(23)\end{aligned}`.

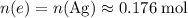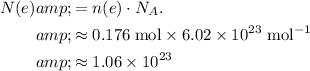Calculate the amount of charge (in coulombs) in that many electrons:

`\begin{aligned}Q &= e\, (n(e)) \\ &\approx 1.602 * 10^(-19)\; \rm C * 1.06 * 10^(23) \\ &\approx 16987.1 \; \rm C \end{aligned}`.

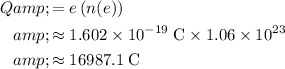A current of
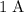`1\; \rm A` carries a charge of
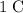`1\; \rm C` every second. Thus, the amount of time required for this current to carry that much electron would be:"

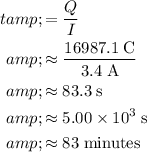`\begin{aligned}t &= (Q)/(I) \\ &\approx (16987.1\; \rm C)/(3.4\; \rm A) \\ &\approx 83.3\; \rm s \\ &\approx 5.00* 10^(3)\; \rm s \\ &\approx 83\; \text{minutes} \end{aligned}`.