Answer:
It's obtuse.
Explanation:
Mumble. Smells al-kashi laws of cosine to me.
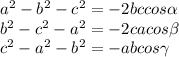
Now, we don't need to calculate the RHSs, and then:
If at least one of the three LHSs is greater than zero, the triangle is obtuse
If at least one is zero, it's a right triangle (pythagorean theorem anyone?)
if all three numbers are less than zero, the triangle is acute
Start crunching numbers.
 First try was the charm. finding 30 means that the product
First try was the charm. finding 30 means that the product
![[-2(√(73))(6) ]cos \alpha](https://img.qammunity.org/2022/formulas/mathematics/high-school/l1hn1b5nzorpqylb7wyl4nfh1q998x7e0v.png) is positive, and since the product in the large bracket is negative, the cosine has to be 0, thus the angle has to be greater than 90°, QED
is positive, and since the product in the large bracket is negative, the cosine has to be 0, thus the angle has to be greater than 90°, QED