Question

HELP ME PLEASE!!!!!!!

Answer 1

x = 18, y = 6

Explanation:

Given the two parallel lines cut through by a transversal, thereby creating perpendicular lines. According to the Perpendicular Transversal Theorem, if a transversal is perpendicular to one of the parallel lines, then it means that the same transversal must also be perpendicular to the other parallel line.

Since perpendicular lines form 90° angles, then it means that each of the angles formed by the intersection of the parallell lines and transversal has a measure of 90°.

Thus, we can infer that (3x + 6y)° = 90°, and (5x)° = 90°.

Solve for x:

Start by dividing both sides by 5 to solve for x:

5x° = 90°

`\large\mathsf{(\:5x^(\circ))/(5)\:=\:(\:90^(\circ))/(5)}`

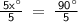
x = 18°

Solve for y:

Substitute the value of x into the (3x + 6y)° to solve for y:

3x° + 6y° = 90°

3(18)° + 6y = 90°

54° + 6y° = 90°

Subtract 54° from both sides:

54° - 54° + 6y° = 90° - 54°

6y° = 36°

Divide both sides by 6 to solve for y:

`\large\mathsf{(\:6y^(\circ))/(6)\:=\:(\:36^(\circ))/(6)}`

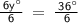
y = 6°

Answers:

Therefore, x = 18, and y = 6.