Question

How can you multiply fractions and mixed numbers?​

Answer 1

Explanation:

In order to multiply fractions and mixed numbers, you must first transform the mixed number into a single fraction (will most likely turn into an improper fraction). An improper fraction is a fraction where the numerator is greater than the denominator.

Example:

Suppose that you were given the following fractions to multiply:

`\large\mathsf{(5)/(7)\:*\:2(3)/(5)}`

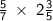
The first step is to transform the mixed fraction,
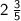`\large\mathsf{2\:(3)/(5)}`, into a single fraction.

You will have to multiply the denominator with the whole number, then add the numerator. The denominator does not change when you do this transformation processs.

The mixed fraction will now turn into the following improper fraction:

`\large\mathsf{2\:(3)/(5)}` ⇒
`\large\mathsf{(13)/(5)}`

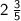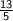
Now, you will be able to multiply
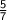`\large\mathsf{(5)/(7)}` and
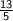`\large\mathsf{(13)/(5)}` together by multiplying the numerator, 5 and 13 and the denominator, 7 and 5.

`\large\mathsf{(5)/(7)\:*\:(13)/(5)\:=\:(5\:*\:13)/(7\:*\:5)\:=\:(65)/(35)}`

Since the product of the two fractions is an improper fraction, it is often customary to express the fraction into its lowest terms. Given the improper fraction,
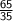`\large\mathsf{(65)/(35)}`, the greatest common factor between 65 and 35 is 5.

Hence, we could simply divide the numerator and the denominator by
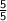`\large\mathsf{(5)/(5)}` to simplify the fraction.

`\large\mathsf{(65)/(35)\:/\:(5)/(5)\:=\:(13)/(7)}`

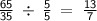
Therefore, the final answer is:
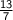`\large\mathsf{(13)/(7)}` . To transform this improper fraction into a mixed number, simply divide its numerator by the denominator, thereby resulting into the following mixed number:
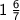`\large\mathsf{1\:(6)/(7)}`.