The correct volume of the sculpture is option D.
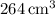 .
.
How did we get the value?
The sculpture consists of a cube and a pyramid. The cube forms the base of the sculpture, and the pyramid is on top of the cube. The total height of the sculpture is given as 10 cm.
1. Cube Volume: The volume
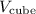 of a cube is calculated using the formula:
of a cube is calculated using the formula:
![\[ V_{\text{cube}} = \text{edge length}^3 \]](https://img.qammunity.org/2023/formulas/mathematics/college/9yql5d7sx5j0xadvgjsxzzhhrk3bkp2yhi.png)
In this case, the edge length of the cube is given as 6 cm. So,
![\[ V_{\text{cube}} = 6^3 \]](https://img.qammunity.org/2023/formulas/mathematics/college/9esbjmi41bcp9prpi1dm5wbtfbx9jkyibl.png)
2. Pyramid Volume:
The volume
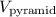 of a pyramid is given by the formula:
of a pyramid is given by the formula:
![\[ V_{\text{pyramid}} = (1)/(3) * \text{base area} * \text{height} \]](https://img.qammunity.org/2023/formulas/mathematics/college/bqtcpa7fuorupcmr2774qevp99bumujkyy.png)
Since the pyramid is sitting on the cube, the base area of the pyramid is equal to the area of the cube's face. The base area of the pyramid is a square, and its side length is the same as the edge length of the cube. So,
![\[ \text{base area} = (\text{edge length})^2 \]](https://img.qammunity.org/2023/formulas/mathematics/college/zi4t7begd40pw4e5lgeyhkkkbgzekesxtb.png)
The height of the pyramid is given as the total height of the sculpture minus the height of the cube:
![\[ \text{height}_{\text{pyramid}} = \text{total height} - \text{height}_{\text{cube}} \]](https://img.qammunity.org/2023/formulas/mathematics/college/3ckxz47u75cn035y34t1cbr48e04aazqg8.png)
Substituting these values into the pyramid volume formula:
![\[ V_{\text{pyramid}} = (1)/(3) * (\text{edge length})^2 * (\text{total height} - \text{height}_{\text{cube}}) \]](https://img.qammunity.org/2023/formulas/mathematics/college/gglqv1wer1hntc03qwnhg7cdvm87es2z1w.png)
3. Total Volume: The total volume
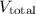 of the sculpture is the sum of the cube volume and the pyramid volume:
of the sculpture is the sum of the cube volume and the pyramid volume:
![\[ V_{\text{total}} = V_{\text{cube}} + V_{\text{pyramid}} \]](https://img.qammunity.org/2023/formulas/mathematics/college/aun37t4gzpy0o0koeybkjczrtrrxb0imxx.png)
Let's substitute the given values into these formulas and calculate the volume:
![\[ V_{\text{cube}} = 6^3 \\ = 216 \, \text{cm}^3 \]](https://img.qammunity.org/2023/formulas/mathematics/college/hj6tt7m0yta9jes438hv12osyc3ybuc0wx.png)
![\[ V_{\text{pyramid}} = (1)/(3) * 6^2 * (10 - 6) \\= (1)/(3) * 36 * 4 \\= 48 \, \text{cm}^3 \]](https://img.qammunity.org/2023/formulas/mathematics/college/znlhrskxlpuvpjln8rt5ijl8i7c1rd8hv9.png)
![\[ V_{\text{total}} = V_{\text{cube}} + V_{\text{pyramid}} \\= 216 + 48 \\= 264 \, \text{cm}^3 \]](https://img.qammunity.org/2023/formulas/mathematics/college/w9h4pqadqthbtv0dsfb6x5hoi739dcarmw.png)
So, the correct volume of the sculpture is option D.
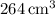 .
.