Question

A hollow sphere of radius 68 cm rolls without slipping to the bottom of an inclined plane. If the angular velocity of the sphere is 5.88 rad/s at the bottom, what is the height of the inclined plane

Answer 1

Hi there!

We know that:

Ei = Ef

At the bottom of the incline, we have both rotational and translational kinetic energy. Recall:

Translational KE = 1/2mv²

Rotational KE = 1/2Iw²

We can begin by deriving an equation for the final energy of the sphere.

Moment of Inertia of a hollow sphere= 2/3mR²

`KE_(total) = (1)/(2)mv^2 + (1)/(2)((2)/(3)mR^2((v^2)/(R^2)))`

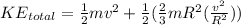
Simplify:

`KE_(total) = (1)/(2)mv^2 + (1)/(3)mv^2 = (5)/(6)mv^2`

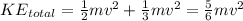
Since Ei = Ef, and the initial energy is simply PE = mgh, thus:

mgh = 5/6mv²

Cancel out 'm':

gh = 5/6v²

We are given the angular velocity, so we can convert to velocity using:

v = ωr

v = 5.88(.68) ≈ 4.00 m/s

h = (5/6v²)/g

h = (5/6(4²))/g = 1.359 m