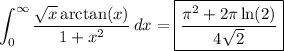Question

`\rm\int^(\infty)_(0) \frac{ √(x) \arctan(x) }{1 + {x}^(2) }\: dx\\`​

Answer 1

Let

`I(a) = \displaystyle \int_0^\infty (\sqrt x \arctan(ax))/(1+x^2) \, dx`

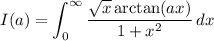
Differentiate with respect to a :

`I'(a) = \displaystyle a \int_0^\infty (x^(\frac32))/((1+x^2)(1+a^2x^2)) \, dx`

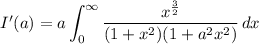
Substitute y = √x :

`I'(a) = \displaystyle 2a \int_0^\infty (y^4)/((1+y)(1+a^2y)) \, dy`

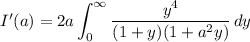
Polynomial division yields

`(y^4)/((1+y)(1+a^2y)) \\\\ = \frac1{a^2}y^2 - \left(\frac1{a^2} + \frac1{a^4}\right)y + \frac1{a^2} + \frac1{a^4} + \frac1{a^6} - \frac{\left(1+\frac1{a^2} + \frac1{a^4} + \frac1{a^6}\right)y + \frac1{a^2} + \frac1{a^4} + \frac1{a^6}}{(1+y)(1+a^2y)}`

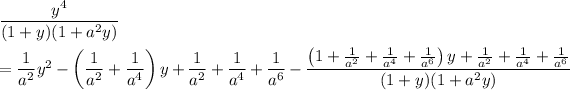
Computing I'(a) isn't so difficult from here. You'd find (assuming a ≥ 0)

`I'(a) = \displaystyle \frac\pi{\sqrt2\left(\sqrt a + a + a^(\frac32) + a^2\right)}`

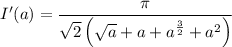
Integrate both sides with respect to a. On the right side, substituting b = √a yields

`\displaystyle \int (da)/(\sqrt a + a + a^(\frac32) + a^2) = \int (2b)/(b + b^2 + b^3 + b^4) \, db \\\\ = 2 \int (db)/(1 + b + b^2 + b^3) \\\\ = 2 \int (db)/((1+b)(1+b^2)) \\\\ = \int \left(\frac1{1+b} + (1-b)/((1+b^2))\right) \, db \\\\ = \frac14 \left(2 \arctan(b) + 2 \ln(1 + b) - \ln(1 + b^2)\right) + C \\\\ = \frac14 \left(2 \arctan(\sqrt a) + 2 \ln(1 + \sqrt a) - \ln(1 + a)\right) + C`

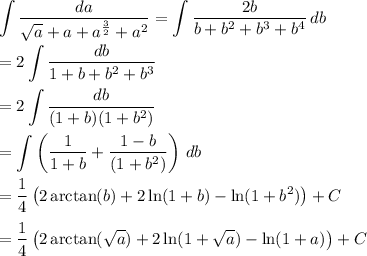
Noting that a = 0 makes the integral I(a) vanish, we have

`0 = \frac14 \left(2 \arctan(\sqrt0) + 2\ln(1 + \sqrt0) - \ln(1 + 0)\right) + C \implies C = 0`

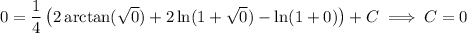
and so

`\displaystyle I(a) = \frac\pi{4\sqrt2} \left(2 \arctan(\sqrt a) + 2 \ln(1 + \sqrt a) - \ln(1 + a)\right)`

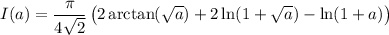
We recover the integral we want with a = 1, which gives a value of

`\displaystyle \int_0^\infty (\sqrt x \arctan(x))/(1 + x^2) \, dx = \boxed{(\pi^2 + 2\pi\ln(2))/(4\sqrt2)}`