Question

`\rm \int_(0)^( \pi ) \cos( \cot(x) - \tan(x)) \: dx \\`​

Answer 1

Replace x with π/2 - x to get the equivalent integral

`\displaystyle \int_(-\frac\pi2)^(\frac\pi2) \cos(\cot(x) - \tan(x)) \, dx`

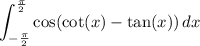
but the integrand is even, so this is really just

`\displaystyle 2 \int_0^(\frac\pi2) \cos(\cot(x) - \tan(x)) \, dx`

Substitute x = 1/2 arccot(u/2), which transforms the integral to

`\displaystyle 2 \int_(-\infty)^\infty (\cos(u))/(u^2+4) \, du`

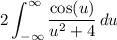
There are lots of ways to compute this. What I did was to consider the complex contour integral

`\displaystyle \int_\gamma (e^(iz))/(z^2+4) \, dz`

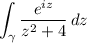
where γ is a semicircle in the complex plane with its diameter joining (-R, 0) and (R, 0) on the real axis. A bound for the integral over the arc of the circle is estimated to be

`\displaystyle \left|\int_(z=Re^(i0))^{z=Re^(i\pi)} f(z) \, dz\right| \le (\pi R)/(|R^2-4|)`

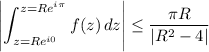
which vanishes as R goes to ∞. Then by the residue theorem, we have in the limit

`\displaystyle \int_(-\infty)^\infty (\cos(x))/(x^2+4) \, dx = 2\pi i {} \mathrm{Res}\left((e^(iz))/(z^2+4),z=2i\right) = \frac\pi{2e^2}`

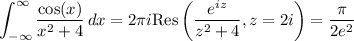
and it follows that

`\displaystyle \int_0^\pi \cos(\cot(x)-\tan(x)) \, dx = \boxed{\frac\pi{e^2}}`