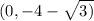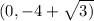Question

Write the equation of a parabola with focus at (1,-4) and a directrix at X=2

Answer 1

The equation of a parabola is

`x = (1)/(4(f - h)) (y - k) ^(2) + h`

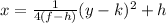
Explanation:

(h,k) is the vertex and (f,k) is the focus.

Thus, f = 1, k = −4.

The distance from the focus to the vertex is equal to the distance from the vertex to the directrix: f - h = h - 2.

Solving the system, we get h = 3/2, k = -4, f = 1.

The standard form is:

`x = - (y ^(2) )/(2) - 4y - (13)/(2)`

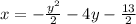
The general form is:

`2x + {y}^(2) + 8y + 13 = 0`

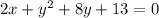
The vertex form is:

`x = - ((y + 4) ^(2) )/(2) + (3)/(2)`

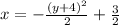
The axis of symmetry is the line perpendicular to the directrix that passes through the vertex and the focus: y = -4.

The focal length is the distance between the focus and the vertex: 1/2.

The focal parameter is the distance between the focus and the directrix: 1.

The latus rectum is parallel to the directrix and passes through the focus: x = 1.

The length of the latus rectum is four times the distance between the vertex and the focus: 2.

The eccentricity of a parabola is always 1.

The x-intercepts can be found by setting y = 0 in the equation and solving for x.

x-intercept:

`( - (13)/(2) \: ,0)`

The y-intercepts can be found by setting x = 0 in the equation and solving for y.

y-intercepts:

`(0, - 4 - √(3))`

`(0, - 4 + √(3))`