Question

Use synthetic division to find the quotient and remainder when - 2x3 + 19x

3 is divided by X-3 by completing the parts below.
(a) Complete this synthetic division table.
3) -2 0 19-3
0 0


0 0
Х
5
Remainder
(b) Write your answer in the following form: Quotient +
X-3
3
- 2x + 19x - 3
X-3
+
X-3

No links

Answer 1

X-3

Explanation: its very makes sense. and easy to understand!

Answer 2

1. The quotient obtained by synthetic division is
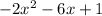`-2x^2 - 6x + 1`, and the remainder is
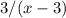`3/(x-3)`. 2. When
`-2x^3 + 19x - 3` is divided by
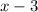`x-3`, the result is
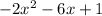`-2x^2 - 6x + 1` with a remainder of
`3/(x-3)`.

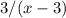1. Let's complete the synthetic division table:

(it has been attached)

2. Now, write the answer in the requested form:

`\[ -2x^3 + 19x - 3 = (-2x^2 - 6x + 1)(x - 3) + (3)/(x-3) \]`

So, the quotient is
`\(-2x^2 - 6x + 1\)` and the remainder is
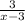`\((3)/(x-3)\)`. Therefore, the answer is:
`\[ (-2x^3 + 19x - 3)/(x - 3) = -2x^2 - 6x + 1 + (3)/(x-3) \]`

In synthetic division, we divide polynomials efficiently using a root of the divisor. In this case,
`-2x^3 + 19x - 3` is divided by
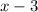`x-3`. The synthetic division table facilitates the process, showing coefficients and remainders.

The quotient,
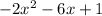`-2x^2 - 6x + 1`, represents the result of the division, and the remainder,
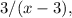`3/(x-3),` is the fraction left over. The expression
`-2x^3 + 19x - 3` can be reconstructed by multiplying the quotient and divisor, adding the remainder to form the original polynomial.