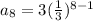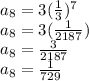Answer:
The 8th term is
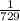 .
.
Explanation:
Let's begin with the formula for a geometric sequence. We know this is geometric because we are working with a common ratio, or the number we multiply to find each term.
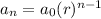
In this formula,
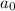 is the first term,
is the first term,
 is the common ratio, and
is the common ratio, and
 is the desired term. We know the values of
is the desired term. We know the values of
 ,
,
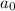 , and
, and
 from the given information:
from the given information:
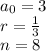
Substituting those values we get: