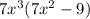Answer:
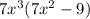
Explanation:
To factor, you have to find the GCF of 49 and 63 and the GCF of
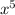 and
and
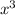
Factor 49: 1,7, and 49
Factor 63: 1, 3, 7, 9, 21, 63
Factor
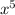 :
:
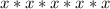
Factor
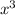 :
:
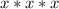
So the GCF of 49 and 63 is 7
The GCF of
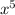 and
and
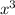 is
is
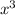
We multiply 7 by
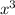 to get
to get
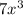
So now we start to factor out the GCF of
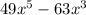
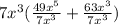
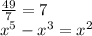
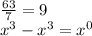 because
because
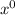 can't be written as an exponent we don't write
can't be written as an exponent we don't write
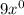
When we factor we get