(3x^(2)+y^(2))Y+(y^(2)-x^(2))x×(dy)/(dx)=0

Question

(3
`x^(2)`+
`y^(2)`)Y+(
`y^(2)`-
`x^(2)`)x×
`(dy)/(dx)`=0

Answer 1

It looks like the given differential equation is

(3x² + y²) y + (y² - x²) x dy/dx = 0

Multiply both sides by 1/x³ to get

(3 + y²/x²) y/x + (y²/x² - 1) dy/dx = 0

(Note that in order to do this, we must have x ≠ 0, which means that if a solution exists, it would have to be on either (-∞, 0) or (0, ∞).)

Now substitute z = y/x, or y = xz, from which we get dy/dx = x dz/dx + z. Making this replacement and simplifying yields a separable equation:

(3 + z²) z + (z² - 1) (x dz/dx + z) = 0

(3 + z²) z + (z² - 1) x dz/dx + (z² - 1) z = 0

(z² - 1) x dz/dx = -(2z³ + 2z)

x dz/dx = (2z³ + 2z)/(1 - z²)

(1 - z²)/(2z (z² + 1)) dz = dx/x

Integrate both sides. On the left, split up the expression into partial fractions.

`(1-z^2)/(z(z^2+1)) = \frac az + (bz+c)/(z^2+1)`

`(1-z^2)/(z(z^2+1)) = (a(z^2+1)+(bz+c)z)/(z(z^2+1))`

`1-z^2 = (a+b)z^2 + cz + a`

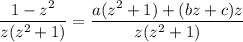
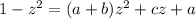
for which we find a = 1, b = -2, and c = 0:

`(1-z^2)/(2z(z^2+1)) = \frac12 \left( \frac1z - (2z)/(z^2+1) \right)`

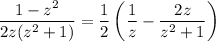
Integrating and simplifying yields

1/2 ∫ (1/z - 2z/(z² + 1)) dz = ∫ dx/x

1/2 (ln|z| - ln(z² + 1)) = ln|x| + C

1/2 ln|z / (z² + 1)| = ln|x| + C

ln(√(z/(z² + 1))) = ln|x| + C

exp[ln(√(z/(z² + 1)))] = exp[ln|x| + C]

√(z/(z² + 1)) = exp[ln|x|] exp[C]

√(z/(z² + 1)) = Cx

z/(z² + 1) = Cx²

Replacing z = y/x then gives us an implicit solution of

(y/x) / (y²/x² + 1) = Cx²

xy / (y² + x²) = Cx²

y / (y² + x²) = Cx

y = Cx (y² + x²)

Cxy² - y + Cx³ = 0

though we can solve for y explicitly (assuming x > 0) using the quadratic formula to end up with

y = (1 + √(1 - Cx⁴))/(Cx)

(the other solution only differs by the sign on the square root)