Question

21.
Ify= 1+x, find
x
dy.
/
dx

Answer 1

A. 2/(1 -x)²

Explanation:

The derivative of a ratio is given by the formula ...

d(u/v) = (v·du =u·dv)/v²

Here, we have ...

u = 1+x; du = 1·dx

v = 1 -x; dv = -1·dx

Then ...

`dy=((1-x)(dx)-(1 +x)(-dx))/((1-x)^2)\\\\(dy)/(dx)=(1-x +1+x)/((1-x)^2)=\boxed{(2)/((1-x)^2)}`

__

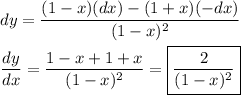
Additional comment

The formula used above is a combination of the power rule and the product rule.

• d(u^-1) = -du·u^-2 = -du/u² . . . . power rule
• d(uv) = u·dv +v·du . . . . . . . . product rule