Answer:
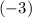 .
.
Explanation:
Over this interval, the change in the value of this function is:
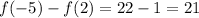 .
.
The corresponding change in the value of
 :
:
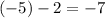 .
.
The average rate of change of function
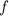 over this interval is equal to the change in the function value divided by the corresponding change in
over this interval is equal to the change in the function value divided by the corresponding change in
 :
:
 .
.
Thus, the average rate of change of
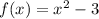 over the interval
over the interval
![[-5,\, 2]](https://img.qammunity.org/2023/formulas/mathematics/college/vcvvmorxovu8lh82jsna437eyai0l6yqp0.png) would be
would be
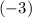 .
.