Question

Helppp(◕દ◕)

find the length of the missing side of the triange ,round to the nearest tenth if necessary​

Answer 1

13 cm

Explanation:

Use Pythagora's theorem to solve for the hypotenuse of the triangle:

`a^2+b^2=c^2`

Where a and b are the two shorter legs, and c is the hypotenuse.

Replace the values in and solve for c:

`5^2+12^2=c^2\\25+144=c^2\\169=c^2\\13=c`

Answer 2

The length of missing side of triangle is 13 cm.

Explanation:

Solution :

Here, we have given that the two sides of triangle are 5 cm and 12 cm.

Finding the third side of triangle by pythagoras theorem formula :

`{\longrightarrow{\pmb{\sf{{(c)}^(2) = {(a)}^(2) + {(b)}^(2)}}}}`

• 
  `\pink\star` a = 5 cm
• 
  `\pink\star` b = 12 cm
• 
  `\pink\star` c = ?

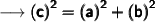
Substituting all the given values in the formula to find the third side of triangle :

`\begin{gathered}\qquad{\longrightarrow{\sf{{(c)}^(2) = {(a)}^(2) + {(b)}^(2)}}}\\\\\qquad{\longrightarrow{\sf{{(c)}^(2) = {(5)}^(2) + {(12)}^(2)}}}\\\\\qquad{\longrightarrow{\sf{{(c)}^(2) = {(5 * 5)} + {(12 * 12)}}}}\\\\\qquad{\longrightarrow{\sf{{(c)}^(2) = {(25)} + {(144)}}}}\\\\\qquad{\longrightarrow{\sf{{(c)}^(2) = 25 + 144}}}\\\\\qquad{\longrightarrow{\sf{{(c)}^(2) = 169}}}\\\\\qquad{\longrightarrow{\sf{c= √(169)}}}\\\\\qquad{\longrightarrow{\sf{c= √(13 * 13)}}}\\\\\qquad{\longrightarrow{\sf{c= 13 \: cm}}}\\\\ \qquad\star{\underline{\boxed{\sf{\red{c= 13 \: cm}}}}}\end{gathered}`

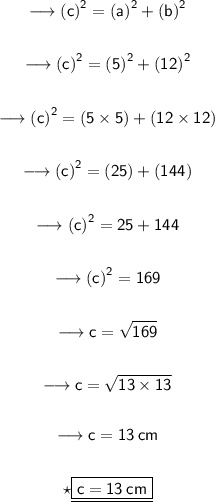
Hence, the length of missing side is 13 cm.

`\rule{300}{2.5}`