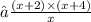STEP1:
Simplify
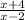
Equation at the end of step1:
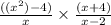
Factoring: x2 - 4
Theory : A difference of two perfect squares, A2 - B2 can be factored into (A+B) • (A-B)
Proof : (A+B) • (A-B) =
A² - AB + BA - B² =
A² - AB + AB - B² =
A² - B²
Note : AB = BA is the commutative property of multiplication.
Note : - AB + AB equals zero and is therefore eliminated from the expression.
Check : 4 is the square of 2
Check : x2 is the square of x1
Factorization is : (x + 2) • (x - 2)
Polynomial Long Division :
2.2 Polynomial Long Division
Dividing : x + 2
("Dividend")
By : x ("Divisor")
dividend x + 2
- divisor * x⁰ x
remainder 2
Quotient : 1
Remainder : 2
Equation at the end of step 2:
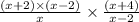
Cancel out (x-2) which appears on both sides of the fraction line.
Final result :