Answer:
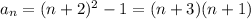
Explanation:
If you add 1 to each number, you get a perfect square: 4, 9, 16, 25, 36, which are the squares of 2, 3, 4, 5, 6...
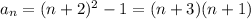
Note that the two expressions are the same, but one might be more convenient than the other if you are manually calculating terms.