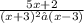STEP1: Equation at the end of step 1
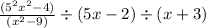
STEP2:
Simplify —
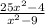
Factoring: 25x2 - 4
Theory : A difference of two perfect squares, A2 - B2 can be factored into (A+B) • (A-B)
Proof : (A+B) • (A-B) =
A² - AB + BA - B² =
A² - AB + AB - B² =
A² - B²
Note : AB = BA is the commutative property of multiplication.
Note : - AB + AB equals zero and is therefore eliminated from the expression.
Check : 25 is the square of 5
Check : 4 is the square of 2
Check : x2 is the square of x1
Factorization is : (5x + 2) • (5x - 2)
Trying to factor as a Difference of Squares:
Factoring: x2 - 9
Check : 9 is the square of 3
Check : x2 is the square of x1
Factorization is : (x + 3) • (x - 3)
Polynomial Long Division :
2.3 Polynomial Long Division
Dividing : 5x + 2
("Dividend")
By : x + 3 ("Divisor")
dividend 5x + 2
- divisor * 5x⁰ 5x + 15
remainder - 13
Quotient : 5
Remainder : -13
Equation at the end of step2:
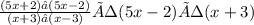
STEP3:
Divide
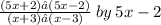
Canceling Out :
3.1 Cancel out (5x - 2) which appears on both sides of the fraction line.
Equation at the end of step3:
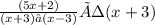
STEP4:
Divide
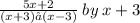
Multiplying Exponential Expressions:
4.1 Multiply (x + 3) by (x + 3)
The rule says : To multiply exponential expressions which have the same base, add up their exponents.
In our case, the common base is (x+3) and the exponents are :
1 , as (x+3) is the same number as (x+3)1
and 1 , as (x+3) is the same number as (x+3)1
The product is therefore, (x+3)¹ = (x+3)²
Final result :