Question

If u understand this stuff, you're an actual genius and should help me :OO

tysm

(straggling in geometry rn)​

Answer 1

I'm assuming sides marked with the same number of cuts are congruent.

Also remember that the internal angles of a triangle sum up to 180, and angles opposite by the vertex are congruent.

13.The left triangle and the right triangle is isosceles. it means the two angles over the vertical line are congruent.
`50+50+x = 180 \rightarrow x= 80`
`y+y+100 = 180 \rightarrow y = 40`

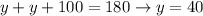
14. Remember that the external angle is the sum of the two internal angles not sharing the vertex. At this point it's a simple system of equation

`\left \{ {{x+y +\\y = 180} \atop {x+y = 110}} \right. \\110 +y=180 \rightarrow y= 70; x =40`

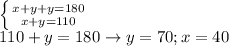
15. y=4 (triangle is isosceles, height and median coincide). Moreover the angle at the middle of the horizontal side is a right angle,
`x+90+52 = 180 \rightarrow x = 38`

16 y=65 (the two angle at the base of an isosceles triangle are congruent). Moreover on the left triangle the other two angles are equal to y( they have the same measure, and the right one is opposed by the vertex)
`x+y+y=180 \rightarrow x +65+65=180 \rightarrow x =50`

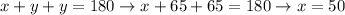
17. Assuming triangle is isosceles - else you would be missing a measure! -
`x +(2x-5) +(2x-5) = 20 \rightarrow 5x=30\rightarrow x = 6`

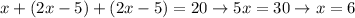
18. Triangle is - you guessed it, isosceles again.
`x+44+44=180 \rightarrow x= 92; y+2 = 7 \rightarrow y = 5`

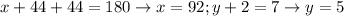
19. Horrible image. I'm assuming that the two sides of the smaller triangle are congruent, as it is the left part of the diagonal longer side of the external triangle.

For the small triangle (did i mention it's isosceles?) 80° is an external angle, so
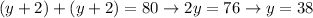`(y+2)+(y+2) = 80 \rightarrow 2y=76 \rightarrow y=38`; for the smaller triangle
`x+80+80 = 180 \rightarrow x = 20`

20. finally. the inner triangle is both isosceles and a right triangle The two angles at the base has to be 45°