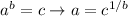Question

18= 1.57(multiply sign) X^2.2

please give me steps!!!

Answer 1

Answer: x = 3.030631 approximately

Step-by-step explanation:

If you want to solve for x, then you could follow these steps:

`18 = 1.57*x^(2.2)\\\\18/1.57 = x^(2.2)\\\\11.464968 \approx x^(2.2)\\\\x^(2.2) \approx 11.464968\\\\x \approx (11.464968)^{(1)/(2.2)}\\\\x \approx 3.030631\\\\`

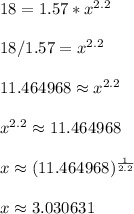
In the second to last step, we have the value 11.464968 raised to the exponent of 1/(2.2) which is done to undo the exponent of 2.2 in the previous line. The rule used is
`a^b = c \to a = c^(1/b)`