Question

Evaluate each finite series for the specified number of terms. 1+2+4+...;n=5

Please show work

Answer 1

31

Explanation:

The series are given as geometric series because these terms have common ratio and not common difference.

Our common ratio is 2 because:

1*2 = 2

2*2 = 4

The summation formula for geometric series (r ≠ 1) is:

`\displaystyle \large{S_n=(a_1(r^n-1))/(r-1)}` or
`\displaystyle \large{S_n=(a_1(1-r^n))/(1-r)}`

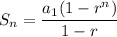
You may use either one of these formulas but I’ll use the first formula.

We are also given that n = 5, meaning we are adding up 5 terms in the series, substitute n = 5 in along with r = 2 and first term = 1.

`\displaystyle \large{S_5=(1(2^5-1))/(2-1)}\\\displaystyle \large{S_5=(2^5-1)/(1)}\\\displaystyle \large{S_5=2^5-1}\\\displaystyle \large{S_5=32-1}\\\displaystyle \large{S_5=31}`

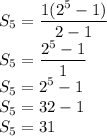
Therefore, the solution is 31.

__________________________________________________________

Summary

If the sequence has common ratio then the sequence or series is classified as geometric sequence/series.

Common Ratio can be found by either multiplying terms with common ratio to get the exact next sequence which can be expressed as
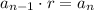`\displaystyle \large{a_(n-1) \cdot r = a_n}` meaning “previous term times ratio = next term” or you can also get the next term to divide with previous term which can be expressed as:

`\displaystyle \large{r=(a_(n+1))/(a_n)}`

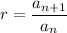
Once knowing which sequence or series is it, apply an appropriate formula for the series. For geometric series, apply the following three formulas:

`\displaystyle \large{S_n=(a_1(r^n-1))/(r-1)}\\\displaystyle \large{S_n=(a_1(1-r^n))/(1-r)}`

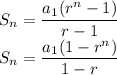
Above should be applied for series that have common ratio not equal to 1.

`\displaystyle \large{S_n=a_1 \cdot n}`

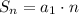
Above should be applied for series that have common ratio exactly equal to 1.

__________________________________________________________

Topics

Sequence & Series — Geometric Series

__________________________________________________________

Others

Let me know if you have any doubts about my answer, explanation or this question through comment!

__________________________________________________________