Question

Find the missing dimension of the cylinder. Volume = 3785 cm^3 height is 19 cm i need to find the radius

​

Answer 1

r ≈ 7.963 cm

Explanation:

Given the following dimensions of a cylinder:

Volume (V) = 3785 cm³

Height (h) = 19 cm

In order to find the value of the radius, it is necessary to determine the formula for finding the radius of a cylinder.

The formula for finding the volume of a cylinder is: V = πr ²h

To isolate the radius, start by dividing both sides by π × h :

`\mathsf{\frac{V} {\pi*\:h}\:=\:\frac{\pi\:r^(2)\:h} {\pi*\:h}}`

`\mathsf{\frac{V} {\pi*\:h}\:=\:r^(2)}`

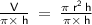
Next, take the square root of both sides to isolate r :

`\mathsf{\sqrt{(V)/(\pi*\:h)} = \sqrt{r^(2)}}`

`\mathsf{\:r\:=\:\sqrt{(V)/(\pi*\:h)}}`

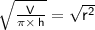
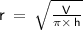
Now, we can finally substitute the given values into the formula for radius, r:

`\mathsf{\:r\:=\:\sqrt{(3785)/(\pi*\:19)}}`

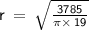
r ≈ 7.963 cm

Therefore, the radius of the cylinder is 7.963 cm.