Answer:
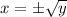
Explanation:
We are given the equation:
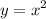
Make ‘x’ the subject of the formula by square root both sides:
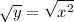
Cancel the square root and square in RHS and write plus-minus in LHS:
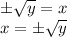
Therefore, the solution is
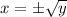
__________________________________________________________
Summary
To make a variable as the subject of equation means to isolate that variable. For an example, if you want to make y as the subject, you’ll have to isolate y-term.
You may also be curious why do you have to add plus-minus on another side when cancelling
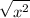 because
because
 and
and
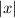 for their positive and their counterparts (opposite/negative) will always give same y-value.
for their positive and their counterparts (opposite/negative) will always give same y-value.
From an example:
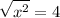 can be rewritten as
can be rewritten as
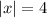 , cancel absolute sign/square root then write plus-minus which the solution is
, cancel absolute sign/square root then write plus-minus which the solution is
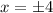 and if you substitute x = 4 or -4, the equation will be true for both values.
and if you substitute x = 4 or -4, the equation will be true for both values.
__________________________________________________________
Others
Let me know if you have any doubts about my answer, explanation or this question through comment!