Question

The area of a rectangular piece of metal is 1,984 square centimeters. The perimeter is 188 centimeters. What are the dimensions of the piece?

Answer 1

There are 2 options:

• x = 32 cm and y = 62 cm

• x = 62 cm and y = 32 cm

Explanation:

That's a rectangular piece, therefore let's consider the width to be x and the length to be y.

A = width * length

1) A = x * y = 1,984 cm^2

P = 2 * (width) + 2 * (length)

2) P = 2x + 2y = 188 cm

Isolate x or y in one of the equations.

xy = 1,984 cm^2

y = 1,984 cm^2 / x

Now plug it in the second equation.

2x + 2y = 188 cm

2x + 2 * (1,984 / x) = 188

Now we have only one variable. Now just solve it alegebraically.

2x + (3,968 / x) = 188

Multiply both sides by x in order to get rid of the fraction.

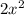`2x^(2)` + 3968 = 188 x

Substract both sides by 188 x

2x^2 + 3968 - 188x = 0

Now divide by 2 to make the equation simpler.

x^2 - 94x + 1984 = 0

use the quadratic formula:

`(94 + √((-94)^2 - 4(1)(1984)) )/(2(1)) = 62\\(94 - √((-94)^2 - 4(1)(1984)) )/(2(1)) = 32`

`x1 = (-b + √(b^2 - 4ac) )/(2a) \\x2 = (-b - √(b^2 - 4ac) )/(2a)`

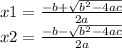
x is either 62 or 32.

let's find y:

y = 1,984 / x

y = 1,984 / 62 = 32

y = 1,984 / 32 = 62

There are 2 options:

• x = 32 cm and y = 62 cm

• x = 62 cm and y = 32 cm