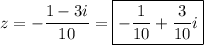How do I determine z ∈ C: ((3-2i)/(1+i) - (5+3i)/(1+2i) )z = (1)/(2) - (2)/(5)i

Question

How do I determine z ∈ C:


`((3-2i)/(1+i) - (5+3i)/(1+2i) )z = (1)/(2) - (2)/(5)i`

Answer 1

Simplify the coefficient of z on the left side. We do this by rationalizing the denominators and multiplying them by their complex conjugates:

`(3-2i)/(1+i) - (5+3i)/(1+2i) = (3-2i)/(1+i)\cdot(1-i)/(1-i) - (5+3i)/(1+2i)\cdot(1-2i)/(1-2i)`

`(3-2i)/(1+i) - (5+3i)/(1+2i) = ((3-2i)(1-i))/(1-i^2) - ((5+3i)(1-2i))/(1-(2i)^2)`

`(3-2i)/(1+i) - (5+3i)/(1+2i) = (3 - 2i - 3i + 2i^2)/(1-(-1)) - (5 + 3i - 10i - 6i^2)/(1-4(-1))`

`(3-2i)/(1+i) - (5+3i)/(1+2i) = \frac{3 - 5i + 2(-1)}2 - \frac{5 - 7i - 6(-1)}5`

`(3-2i)/(1+i) - (5+3i)/(1+2i) = \frac{1 - 5i}2 - \frac{11 - 7i}5`

`(3-2i)/(1+i) - (5+3i)/(1+2i) = \frac{1 - 5i}2\cdot\frac55 - \frac{11 - 7i}5\cdot\frac22`

`(3-2i)/(1+i) - (5+3i)/(1+2i) = (5 - 25i - 22 + 14i)/(10)`

`(3-2i)/(1+i) - (5+3i)/(1+2i) = -(17 + 11i)/(10)`

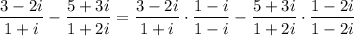
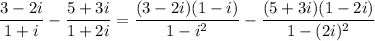
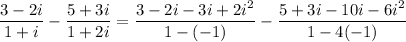
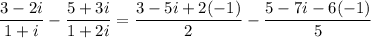
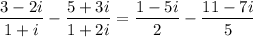
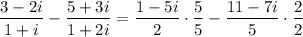
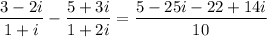
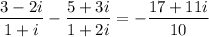
So, the equation is simplified to

`-(17+11i)/(10) z = \frac12 - \frac{2i}5`

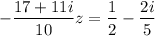
Let's combine the fractions on the right side:

`\frac12 - \frac{2i}5 = \frac12\cdot\frac55 - \frac{2i}5\cdot\frac22`

`\frac12 - \frac{2i}5 = (5-4i)/(10)`

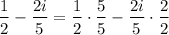
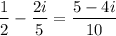
Then

`-(17+11i)/(10) z = (5-4i)/(10)`

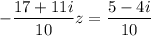
reduces to

`-(17+11i) z = 5-4i`

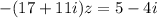
Multiply both sides by -1/(17 + 11i) :

`(-(17+11i))/(-(17+11i)) z = (5-4i)/(-(17+11i))`

`z = -(5-4i)/(17+11i)`

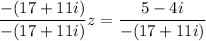
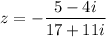
Finally, simplify the right side:

`-(5-4i)/(17+11i) = -(5-4i)/(17+11i) \cdot (17-11i)/(17-11i)`

`-(5-4i)/(17+11i) = -((5-4i)(17-11i))/(17^2-(11i)^2)`

`-(5-4i)/(17+11i) = -(85 - 68i - 55i + 44i^2)/(289-121(-1))`

`-(5-4i)/(17+11i) = -(85 - 68i - 55i + 44(-1))/(410)`

`-(5-4i)/(17+11i) = -(41 - 123i)/(410)`

`-(5-4i)/(17+11i) = -(41 - 41\cdot3i)/(410)`

`-(5-4i)/(17+11i) = -(1 - 3i)/(10)`

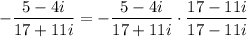
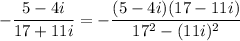
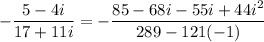
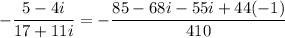
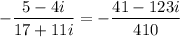
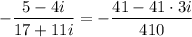
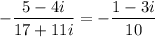
So, the solution to the equation is

`z = -(1-3i)/(10) = \boxed{-\frac1{10} + \frac3{10}i}`