Question

In Fig. 10-41, two blocks, of mass m1 400 g and m2 600 g, are connected by a massless cord that is wrapped around a uniform disk of mass M 500 g and radius R 12.0 cm.The disk can rotate without friction about a fixed horizontal axis through its center; the cord cannot slip on the disk.The system is released from rest. Find (a) the magnitude of the acceleration of the blocks, (b) the tension T1 in the cord at the left, and (c) the tension T2 in the cord at the right

Answer 1

Hi there!

(a)

Assuming this is an Atwood machine, we can begin by summing torques about the axis.

Στ = RT2 - RT1

To eliminate the Rs and solve for acceleration, we can rewrite the expression and express alpha as a/r:

Iα = RT2 - RT1

Moment of Inertia of disk = I = 1/2MR²

1/2MR²(a/R) = R(T2 - T1)

Cancel out the Rs:

1/2Ma = T2 - T1

Now, we must sum FORCES:

∑F1 = T1 - m1g

∑F2 = m2g - T2

Rearrange to solve for tension:

T1 = m1a + m1g

T2 = m2g - m2a

Substitute into the above equation:

1/2Ma = m2g - m2a - m1a - m1g

Solve for a:

1/2Ma + m2a + m1a = m2g - m1g

`a = (g(m2-m1))/((1)/(2)M + m2 + m1)`

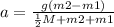
Plug in given values:

`a = (g(.6-.4))/((1)/(2)0.5 + 0.4 + 0.6) = 1.568 m/s^2`

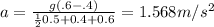
a = 1.568 m/s²

(b)

Plug this acceleration into the equation for T1:

T1 = m1a + m1g = .4(1.568) + .4(9.8) = 4.547 N

(c)

Plug the acceleration into the equation for T2:

T2 = m2g - m2a = .6(9.8) - .6(1.568) = 4.939 N