Question

F(x)=2x^2 + x - 6/ x-1

Answer 1

See below

Explanation:

Zeroes:

`f(x)=(2x^2+x-6)/(x-1)`

`0=(2x^2+x-6)/(x-1)`

`0=2x^2+x-6`

`0=(2x-3)(x+2)`

`x=(3)/(2),-2`

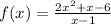
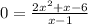
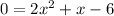
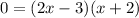
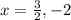
Vertical and Horizontal Asymptotes:

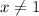`x\\eq 1` is excluded from the domain, therefore, there's a vertical asymptote at
`x=1`

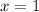
No horizontal asymptotes as the degree of the numerator is greater than the degree of the denominator by 1.

Oblique (Slant) Asymptote:

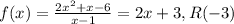`f(x)=(2x^2+x-6)/(x-1)=2x+3,R(-3)`, so the oblique/slant asymptote is
`y=2x+3`