Answer:
A)
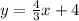
Explanation:
Write the slope formula:
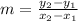
________________________________________________________
Substitute and calculate
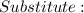
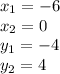
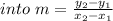
Substitute
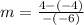
Determine the sign
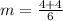
Calculate the sum or difference
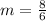
Cross out the common factor
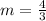
________________________________________________________
Substitute and calculate
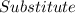
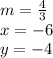
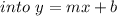
Substitute
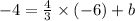
Reduce the expression to the lowest term
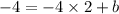
Calculate the product or quotient

Rearrange variables to the left side of the equation
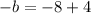
Calculate the sum or difference
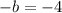
Divide both sides of the equation by the coefficient of variable
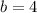
________________________________________________________
Substitute
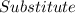
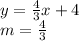
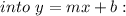
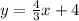
________________________________________________________
Rewrite the equation of the line
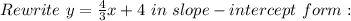
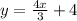
I hope this helps you
:)