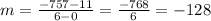Question

Given the function h(x) = -22 + 4x + 11, determine the average rate of change of the function over the interval 0 < x < 6. Answer: Submit Answer attempt to​

Answer 1

Explanation:

First of all, I'm going to assume that you accidentally left out an x-squared term on that -22. Going with that assumption, the average rate of change is the same thing as the slope between 2 points on that graph. It's parabolic, so there is no slope anywhere that is constant except for at a line that is tangent to a point. Our line is a secant line, not a tangent line. Since that is calculus and finds the instantaneous rate of change, I'm assuming that this is not calculus. The method is simple: plug 0 in for x in the function and you'll get a y value for that x; plug 6 in for x and you'll get a y value for that x. Then you plug both those coordinates into the slope formula to find the slope between the 2 points on the graph.

`h(0)=-22(0)^2+4(0)+11\\h(0)=11--->(0,11)\\h(6)=-22(6)^2+4(6)+11\\h(6)=-757`

That gives us the coordinate (6, -757). Plugging into the slope formula:

`m=(-757-11)/(6-0)=(-768)/(6)=-128`