Question

Is anyone can do this?

Answer 1

Surface of
`35,875.86 cm^2`

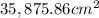
Voliume of
`234,671.58 cm^3`

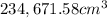
Long and painful calculations

Ok, this is going to take some time. The volume is the sum of all the solids, minus the half cylinder that makes the "tunnel" beneath it. That said, we can split the item into 3 main shapes, and the cylinder: The pyramid in the top left, the square based prism below the pyramid, and the trapezoid prism to the right. I edited a bit the image with paint to add measurements. It's paint so quality is what it is and deal with comic sans as a font.

Let's find the total surface first. We have the surface of the four faces of the pyramid, which are triangles of base 54 and height (red line)
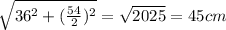`\sqrt{36^2+(\frac{54}2)^2} =√(2025)=45cm`, givins us a total area of
`4* \frac{bh}2 = 2* 45* 54 = 4860 cm^2`

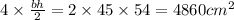
We add the two lateral faces of the left prism: they are two rectangles of side length 70 and 54, for a total area of
`2(70)(54) = 7580 cm^2`

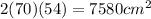
Take the rectangle to the side of the prism, of sides 54 and 70-34 = 36, giving an area of
`54* 36 = 1944 cm^2`

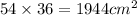
Pick the inclined "roof" of the right prism, again a rectangles, sides 54 and 61: surface is
`3294 cm^2`

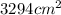
Two side faces of the right building: first pick the height (magenta line), with pythagorean theorem again, equal to
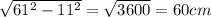`√( 61^2-11^2) = √(3600) = 60 cm`. The surface becomes
`2 \frac{(B+b)h}2 = (34+45)(60)= 4740 cm^2`

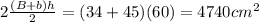
Missing the short sides and the half cylinder making the gallery. The sides - if you imagine un-hinging one and attaching to the bottom of the other - will make a rectangle of sides (45+70) cm and 54 cm with a circular hole in the middle. surface is
`(45+70)*54 - \pi(54/2)^2 =`
`3920.94 cm^2`.

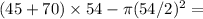
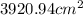Finally, the half cylinder. It's a "rectangle) tall (60+54) cm - the length of the whole contraption, and long half the circle, or
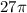`27\pi`. It's surface is
`(60+54)*\27\pi = 9664.92 cm^2`

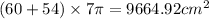
Done with surfaces. At this point we just add everything together. Grab a calculator and start adding up, if I didn't miss anything the total surface will be
`35875.86 cm^2`

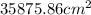
Volumes now. You wished this was over? I totally did.

Bulk of the calculations are done luckly. It's just to cut and paste here and there.

Pyramid first. We know the side length, we know the height, volume is the usual formula

`\frac 13l^2h = \frac 13 54^2* 36= 33,048 cm^3`

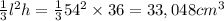
Cube beneath. This one is also easy Sides are 54cm, 54cm and 70cm, volume is their product:

`54*54*70= 204,120 cm^3`

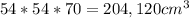
Side prism now: again base surface times height, let's use the trapezoid as a base since we already have the area from above:

`A_th = 2370*54 = 127,980 cm^3`

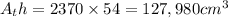
From this we take half a cylinder of radius 27 tall as the whole structure is long.
`\frac12 \pi r^2h = \frac12 \pi (27)^2(60+54) = 130,476.42 cm^3`

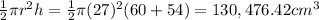
We're done. Let's add the volume of the first 3 solids and subtract the last one - hope you have your calculator handy, to get in total a volume of
`234,671.58 cm^3`

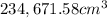
Double and triple check numbers, even if I rand them with excel.