Question

Find the solution to the system of equations:

7x-8y=-23

7x-7y=-14

Answer 1

Solutions: x = 7, y = 9; or (7, 9)

Explanation:

Given the following systems of linear equations:

7x - 8y = -23

7x - 7y = -14

Since the coefficients of x in the given system have the same sign, we could use the process of elimination by subtracting the two equations.

7x - 8y = -23

- 7x - 7y = -14

-y = -9

Divide both sides by -1 to solve for y:

`(-y)/(-1) = (-9)/(-1)`

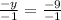
y = 9

Substitute the value of y into either one of the given equations to solve for x:

7x - 7y = -14

7x - 7(9) = -14

7x - 63 = -14

Add 63 to both sides:

7x - 63 + 63 = -14 + 63

7x = 49

Divide both sides by 7 to solve for x:

`(7x)/(7) = (49)/(7)`

x = 7

Double-check whether x = 7 and y = 9 are valid solutions to the given system:

x = 7, y = 9:

7x - 8y = -23

7(7) - 8(9) = -23

49 - 72 = -23

-23 = -23 (True statement).

7x - 7y = -14

7(7) - 7(9) = -14

49 - 63 = -14

-14 = -14 (True statement).

Therefore, the solution to the given systems of linear equations are x = 7, and y = 9, or (7, 9).